How to Determine if a Relationship is a Function
- Ms. Pushpa

- Nov 25, 2016
- 2 min read
Updated: Aug 19, 2020
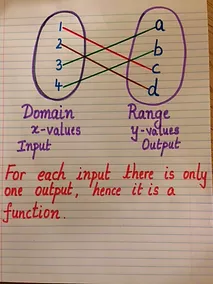
A relation is the mapping between a set of input values called the domain and a set of output values called the range. The input values or the domain consists of the x values of the ordered pair and the output values or range consists of the y values of the ordered pair.
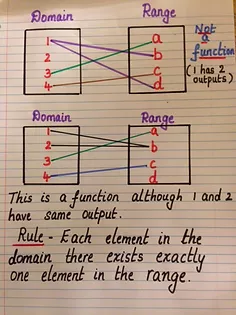
A function is a relation between a given set of elements such that for each element in the domain there exists exactly one element in the range. So how do we determine whether a relation is a function?
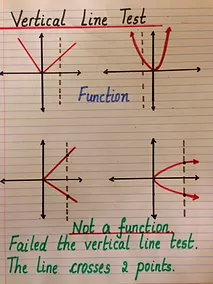
The vertical line test is a visual method used to determine whether a relation represented as a graph is a function. To apply a vertical line test, consider all of the vertical lines that could be drawn on the graph of a relation. If any of the vertical lines intersect
the graph of the relation at more than one point, then the relation is not a function.
Why does the vertical line test work? Well, if the vertical line crosses two points, that means that a given x-value has two y-values that correspond to it. In other words, a given input (x) has more than one output (y). For a relation to be a function, each input can only have one output.
A discrete graph is a graph of isolated points. A discrete function allows the x-values to be only certain points in the interval, usually only integers or whole numbers.
Examples: • The number of people in your class (no fractional parts of a person). • The number of TV sets in a home (no fractional parts of a TV set). • The number of puppies in a liter (no fractional puppies). • The number of questions on a math test (no incomplete questions).
A continuous graph is a graph of points that are connected by a line or smooth curve on the graph. Continuous graphs have no breaks.A continuous function allows the x-values to be ANY points in the interval, including fractions, decimals, and irrational values.
Examples:
• The height of a horse (could be any value within the range of horse heights).
• Time to complete a task (which could be measured to fractions of seconds).
• The outdoor temperature at noon (any value within possible temperatures ranges.)
• The speed of a car on Route 3 (assuming legal speed limits).
Question to think about: Could we determine whether a relation is a function using a horizontal line test? Why or why not? Comment down below!





Comments